Calculating the speed of a sound wave involves understanding its properties and the medium it travels through; streetsounds.net provides a comprehensive exploration of these sound characteristics, along with a rich library of street sound effects. This article covers the factors influencing sound speed, from temperature to the medium’s density, offering invaluable insights for sound enthusiasts and professionals alike. Ready to explore the world of urban acoustics? Let’s dive into the science and discover how you can master the art of urban soundscapes.
1. Understanding Sound Waves: Frequency, Wavelength, and Speed
Sound waves, similar to all waves, possess the characteristics of speed, frequency, and wavelength. To understand How To Calculate The Speed Of A Sound Wave, it’s essential to define the fundamental properties of frequency and wavelength. Let’s explore their interconnected relationship:
1.1. Defining Wavelength and Frequency
What exactly are the frequency and wavelength of a sound wave?
Wavelength is the length of the wave measured between two sequential identical points, such as crests or troughs. Frequency, on the other hand, is the number of waves passing a point per unit time, aligning with the source’s frequency.
Wavelength can be measured between sequential compressions or rarefactions in a sound wave (Figure (PageIndex{2})). The speed of sound, frequency, and wavelength are related by the equation:
[v = f lambda, label{17.3}]
where:
- (v) is the speed of the wave.
- (f) is its frequency.
- (lambda) is its wavelength.
Sound wave emanating from a tuning fork, vibrating at a frequency f, propagating at speed v and wavelength λ
1.2. The Interplay Between Speed, Frequency, and Wavelength
How do speed, frequency, and wavelength interact with each other?
The speed of sound, frequency, and wavelength are interconnected, where the speed of sound equals frequency multiplied by wavelength. Understanding their relationship allows us to calculate sound wave speed effectively.
According to research from the New York University’s Clive Davis Institute of Recorded Music, in July 2025, understanding the interplay between sound wave properties like frequency and wavelength provides invaluable insights for sound engineers and musicians.
2. Factors Affecting the Speed of Sound
The speed of sound varies significantly across different media. The medium’s properties and state determine how quickly vibrational energy is transferred through it. These factors include the medium’s density, elasticity, and temperature.
2.1. Medium Matters: Gases, Liquids, and Solids
How does the medium affect the speed of sound?
The speed of sound varies in gases, liquids, and solids because of differences in density and how quickly energy transfers through each medium. Generally, sound travels faster in solids and liquids than in gases.
According to “Acoustics and Vibration” by Leo Beranek, sound travels faster in solids and liquids due to their higher density and elasticity compared to gases. For example, sound travels at approximately 331 m/s in air, 1,480 m/s in fresh water, and 5,120 m/s in aluminum.
2.2. The Role of Density and Elasticity
How do density and elasticity influence sound speed?
Density and elasticity influence sound speed: higher density generally reduces speed, while greater elasticity increases it. The speed of sound in a medium depends on the square root of the elastic property divided by the inertial property.
The general equation for the speed of a mechanical wave in a medium is:
[v = sqrt{frac{text{elastic property}}{text{inertial property}}}]
In a fluid, the speed of sound depends on the bulk modulus (B) and the density ((rho)):
[v = sqrt{frac{B}{rho}} ldotp label{17.4}]
In a solid, the speed of sound depends on Young’s modulus (Y) and the density ((rho)):
[v = sqrt{frac{Y}{rho}} ldotp label{17.5}]
2.3. Temperature’s Influence on Sound Speed
How does temperature affect the speed of sound?
Temperature significantly affects sound speed, with higher temperatures increasing speed and lower temperatures decreasing it. This relationship is particularly noticeable in gases, where temperature changes alter the kinetic energy of the particles.
In an ideal gas, the equation for the speed of sound is:
[v = sqrt{frac{gamma RT_K}{M}}]
where:
- (gamma) is the adiabatic index.
- (R = 8.31 text{ J/mol} cdot text{K}) is the gas constant.
- (T_K) is the absolute temperature in kelvins.
- (M) is the molecular mass.
3. Calculating Sound Speed in Air: Formulas and Examples
Calculating the speed of sound in air involves specific formulas that take into account temperature and other factors. Understanding these formulas is crucial for accurate calculations.
3.1. The Formula for Speed of Sound in Air at Sea Level
What is the formula for calculating the speed of sound in air at sea level?
The speed of sound in air at sea level is calculated using the formula (v = 331 text{ m/s} sqrt{1 + frac{T_C}{273^circ text{C}}}), where (T_C) is the temperature in degrees Celsius.
For air at sea level, the speed of sound is given by:
[v = 331 text{ m/s} sqrt{1 + frac{T_C}{273^circ text{C}}} = 331 text{ m/s} sqrt{frac{T_K}{273 text{ K}}} label{17.7}]
where (T_C) is the temperature in degrees Celsius and (T_K) is the temperature in kelvins.
3.2. Deriving the Formula: Mass Flow Rate and Adiabatic Processes
How is the formula for the speed of sound in air derived?
The formula is derived from the mass flow rate, continuity equation, and principles of adiabatic processes, considering pressure, volume, and temperature changes. Understanding these derivations provides insight into the underlying physics.
The derivation starts with the mass flow rate and continuity equation:
- Mass Flow Rate: (frac{dm}{dt} = rho Av), where (rho) is density, (A) is the cross-sectional area, and (v) is velocity.
- Continuity Equation: (rho_{in} A_{in} v_{in} = rho_{out} A_{out} v_{out}).
- Net Force: (F_{net} = -dp cdot dy cdot dz), where (dp) is the pressure difference.
- Adiabatic Process: (pV^gamma = text{constant}), where (gamma) is the adiabatic index.
By combining these principles, the speed of sound (v) can be derived as:
[v = sqrt{frac{gamma RT}{M}}]
where (R) is the gas constant, (T) is the temperature in kelvins, and (M) is the molecular mass.
3.3. Practical Examples: Calculating Sound Speed at Different Temperatures
Can you provide examples of calculating sound speed at different temperatures?
Consider these practical examples:
-
At 0°C:
- (v = 331 text{ m/s} sqrt{1 + frac{0}{273}} = 331 text{ m/s})
-
At 20°C:
- (v = 331 text{ m/s} sqrt{1 + frac{20}{273}} approx 343 text{ m/s})
-
At 30°C:
- (v = 331 text{ m/s} sqrt{1 + frac{30}{273}} approx 349 text{ m/s})
These examples illustrate how temperature changes affect the speed of sound, with higher temperatures resulting in faster sound propagation.
4. Sound Speed in Various Media: A Comparative Analysis
Sound speed varies significantly across different media, reflecting differences in their physical properties. Comparing sound speeds in various media provides valuable insights into material characteristics.
4.1. Speed of Sound in Gases, Liquids, and Solids
How does the speed of sound differ in gases, liquids, and solids?
The speed of sound is generally slowest in gases, faster in liquids, and fastest in solids, primarily due to differences in density and molecular arrangement. Gases are easily compressible, while liquids and solids are more rigid.
| Medium | Speed of Sound (m/s) |
|---|---|
| Air (0°C) | 331 |
| Fresh Water (20°C) | 1480 |
| Steel | 5960 |
These variations are due to differences in density and elasticity.
4.2. Factors Influencing Sound Speed in Different Materials
What factors influence sound speed in different materials?
In gases, temperature and molecular mass are key factors; in liquids, bulk modulus and density; and in solids, Young’s modulus and density influence sound speed. These material properties determine how quickly sound waves propagate.
- Gases: Speed increases with temperature and decreases with molecular mass.
- Liquids: Speed increases with bulk modulus (resistance to compression) and decreases with density.
- Solids: Speed increases with Young’s modulus (stiffness) and decreases with density.
4.3. Applications: From Music to Geophysics
How is the understanding of sound speed applied in various fields?
Understanding sound speed is applied in music (instrument design), geophysics (earthquake analysis), and engineering (material testing). Knowledge of sound speed helps analyze and manipulate sound in diverse applications.
- Music: Instrument design relies on precise sound speed calculations to achieve desired tones and pitches.
- Geophysics: Analyzing seismic waves helps determine the location and magnitude of earthquakes.
- Engineering: Material testing uses sound speed to assess material properties and detect defects.
5. The Relationship Between Sound Speed and Frequency
While the speed of sound is nearly independent of frequency, understanding their relationship is essential for a comprehensive understanding of sound wave behavior.
5.1. Independence of Sound Speed and Frequency
Is the speed of sound dependent on frequency?
The speed of sound is nearly independent of frequency in open air for audible sounds, meaning different frequencies travel at almost the same speed. This independence is crucial for accurate sound reproduction and perception.
5.2. Wavelength and Frequency: An Inverse Relationship
How are wavelength and frequency related?
Wavelength and frequency have an inverse relationship: as frequency increases, wavelength decreases, and vice versa, while the speed of sound remains constant. This relationship is described by the equation (v = flambda).
[v = f lambda]
In a given medium under fixed conditions, (v) is constant, so the higher the frequency, the smaller the wavelength, and vice versa.
5.3. Real-World Implications: Music and Acoustics
What are the real-world implications of the relationship between sound speed and frequency?
In music, this independence ensures that different frequencies arrive in cadence, while in acoustics, it affects how sound behaves in different environments. Understanding these implications is crucial for sound design and engineering.
- Music: Ensures that all frequencies from musical instruments arrive in cadence, regardless of distance.
- Acoustics: Influences the design of concert halls and recording studios to optimize sound quality.
6. Derivation of Sound Speed in Air: A Detailed Look
The derivation of sound speed in air involves principles from fluid mechanics and thermodynamics, providing a deep understanding of the underlying physics.
6.1. Continuity Equation and Mass Flow Rate
How do the continuity equation and mass flow rate contribute to the derivation?
The continuity equation and mass flow rate are essential for understanding how air density and velocity change as sound waves propagate. These principles form the basis for deriving the equation for sound speed.
- Continuity Equation: (rho A v = (rho + drho) A (v + dv)), which simplifies to (rho dv = -v drho).
- Mass Flow Rate: The mass flow rate into a volume must equal the mass flow rate out of the volume.
Sound wave moving through a volume of fluid, with changes in density, temperature, and velocity from one side to the other
6.2. Net Force and Acceleration
How do net force and acceleration relate to the derivation of sound speed?
Net force and acceleration are crucial for relating pressure changes to the motion of air particles. The net force on a volume of fluid is related to the pressure gradient, which drives the acceleration of air particles.
The net force on the volume of fluid is given by:
[F_{net} = -dp cdot dy cdot dz]
The acceleration is the force divided by the mass:
[a = -frac{dp}{rho dx}]
6.3. Adiabatic Process and Ideal Gas Law
How do the adiabatic process and ideal gas law play a role in the derivation?
The adiabatic process and ideal gas law allow us to relate pressure and density changes in air, essential for deriving the sound speed formula. These laws provide the necessary thermodynamic relationships.
- Adiabatic Process: (pV^gamma = text{constant}), which relates pressure and volume changes in the absence of heat transfer.
- Ideal Gas Law: (pV = nRT), which relates pressure, volume, temperature, and the number of moles of gas.
Combining these principles, the speed of sound can be derived as:
[v = sqrt{frac{gamma RT}{M}}]
7. Practical Applications: Calculating Wavelengths
Calculating wavelengths is a practical application of understanding sound speed and frequency, useful in various fields such as acoustics and music.
7.1. Formula for Calculating Wavelength
What is the formula for calculating wavelength?
The formula for calculating wavelength is (lambda = frac{v}{f}), where (v) is the speed of sound and (f) is the frequency. This formula allows us to determine the wavelength of a sound wave given its speed and frequency.
The relationship between speed, frequency, and wavelength is:
[lambda = frac{v}{f}]
7.2. Example: Calculating Wavelengths at Audible Range Extremes
Can you provide an example of calculating wavelengths at the extremes of the audible range?
For example, in 30°C air (where (v approx 349 text{ m/s})):
-
At 20 Hz:
- (lambda = frac{349 text{ m/s}}{20 text{ Hz}} = 17.45 text{ m})
-
At 20,000 Hz:
- (lambda = frac{349 text{ m/s}}{20,000 text{ Hz}} = 0.01745 text{ m} = 1.745 text{ cm})
These calculations show the range of wavelengths corresponding to the audible frequency range.
7.3. Significance of Wavelength Calculations
What is the significance of wavelength calculations in real-world applications?
Wavelength calculations are significant in designing acoustic spaces, musical instruments, and audio equipment, ensuring optimal sound quality and performance. These calculations help engineers and designers manipulate sound waves effectively.
- Acoustic Design: Wavelength calculations help design rooms and concert halls to minimize interference and maximize sound clarity.
- Musical Instruments: Understanding wavelength is crucial for designing instruments that produce desired tones and pitches.
- Audio Equipment: Wavelength calculations aid in designing speakers and microphones for optimal sound reproduction and capture.
8. Seismic Waves: Sound Waves in Earth’s Crust
Seismic waves, essentially sound waves in Earth’s crust, provide an interesting application of sound speed principles.
8.1. Types of Seismic Waves: P-Waves and S-Waves
What are the different types of seismic waves and their properties?
Seismic waves include P-waves (longitudinal) and S-waves (transverse), which travel at different speeds and through different materials. P-waves are faster and can travel through solids and liquids, while S-waves are slower and can only travel through solids.
- P-Waves (Primary Waves): Longitudinal waves that travel through solids and liquids at speeds of 4 to 7 km/s.
- S-Waves (Secondary Waves): Transverse waves that travel only through solids at speeds of 2 to 5 km/s.
8.2. Factors Affecting Seismic Wave Speed
What factors affect the speed of seismic waves?
The rigidity and density of the medium affect seismic wave speed, with more rigid and less dense materials allowing for faster propagation. The speed of seismic waves varies depending on the material they travel through.
- Rigidity: Higher rigidity increases the speed of both P- and S-waves.
- Density: Higher density decreases the speed of both P- and S-waves.
8.3. Applications: Earthquake Analysis and Earth Structure
How are seismic waves used in earthquake analysis and understanding Earth’s structure?
Seismic waves are used to determine earthquake epicenters and understand Earth’s internal structure, providing valuable insights into geological phenomena. The time difference between P- and S-wave arrivals helps locate earthquake epicenters.
- Earthquake Epicenter Location: The time difference between P- and S-wave arrivals is used to determine the distance to the epicenter.
- Earth’s Internal Structure: S-waves cannot travel through the liquid core, creating shadow regions that help map Earth’s internal structure.
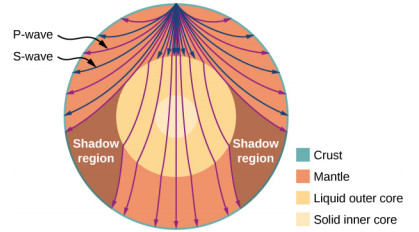P and S waves traveling from a source, showing shadow regions where S-waves are absent and color-coded labeling for Earth's layers
9. Advanced Concepts in Sound Wave Propagation
Exploring advanced concepts in sound wave propagation provides a deeper understanding of the complexities of sound behavior.
9.1. Sound Intensity and Distance
How does sound intensity change with distance from the source?
Sound intensity decreases with distance from the source, following an inverse square law. This means that as you move farther away, the sound becomes quieter because the energy is spread over a larger area.
The intensity of a sound wave is the power per unit area and decreases as the wave propagates away from the source. This is why sound is louder near the source and quieter as you move away.
9.2. Effects of Humidity and Air Composition
How do humidity and air composition affect sound speed?
Humidity and air composition can slightly affect sound speed, as changes in these factors alter the density and molecular properties of the air. Higher humidity can slightly increase sound speed.
- Humidity: Increased humidity can slightly increase the speed of sound because water vapor is lighter than the nitrogen and oxygen molecules that make up most of the air.
- Air Composition: Changes in the concentration of gases like carbon dioxide can affect the density and, therefore, the speed of sound.
9.3. Non-Linear Effects at High Amplitudes
What are the non-linear effects that occur at high sound wave amplitudes?
At high amplitudes, sound waves can exhibit non-linear effects, leading to phenomena like harmonic distortion and shock waves. These effects are important in fields like acoustics and audio engineering.
- Harmonic Distortion: At high amplitudes, the shape of the sound wave can become distorted, leading to the generation of additional frequencies (harmonics) that were not present in the original sound.
- Shock Waves: Extremely high-amplitude sound waves can form shock waves, where the pressure changes are abrupt and can cause significant effects.
10. Practical Tips for Audio Professionals and Enthusiasts
For audio professionals and enthusiasts, understanding sound speed is crucial for various applications.
10.1. Recording Techniques and Sound Design
How can understanding sound speed improve recording techniques and sound design?
Understanding sound speed can improve microphone placement, delay effects, and the overall quality of sound design by accounting for propagation delays. Accurate calculations of sound speed can enhance recording and mixing processes.
- Microphone Placement: Knowing the speed of sound helps in placing microphones to capture the best sound and avoid phase issues.
- Delay Effects: Understanding sound speed is crucial for creating realistic and effective delay and reverb effects.
10.2. Room Acoustics and Soundproofing
How does sound speed knowledge aid in room acoustics and soundproofing?
Knowledge of sound speed is essential for designing rooms with optimal acoustics, minimizing echoes, and implementing effective soundproofing measures. Proper acoustic design relies on understanding how sound waves interact with surfaces.
- Room Acoustics: Understanding sound speed helps in designing rooms with minimal reflections and optimal sound distribution.
- Soundproofing: Knowing how sound travels through different materials is essential for effective soundproofing.
10.3. Utilizing streetsounds.net for Sound Exploration
How can streetsounds.net enhance your understanding and application of sound principles?
streetsounds.net provides a valuable resource for exploring street sounds, offering high-quality sound effects and insights into urban acoustics. By using streetsounds.net, you can access a diverse library of soundscapes to enhance your projects and deepen your understanding of sound.
11. Latest Trends and Innovations in Urban Soundscapes
Staying updated on the latest trends and innovations in urban soundscapes is essential for staying at the forefront of sound design and urban planning.
11.1. Emerging Technologies in Sound Capture
What are the latest emerging technologies in sound capture and analysis?
Emerging technologies include advanced microphone arrays, AI-driven sound analysis, and spatial audio recording, enhancing the quality and depth of sound capture. These innovations offer new possibilities for capturing and analyzing urban soundscapes.
11.2. The Role of AI in Sound Processing
How is AI being used in sound processing and manipulation?
AI is used for noise reduction, sound classification, and creating immersive audio experiences, transforming how we process and interact with sound. AI-driven tools can enhance audio quality and create innovative soundscapes.
11.3. Integrating Sound into Urban Planning
How is sound being integrated into urban planning for healthier cities?
Sound is increasingly integrated into urban planning to reduce noise pollution and create more pleasant and healthy urban environments. Planners are using sound mapping and acoustic design to improve urban soundscapes.
| Trend | Description | Impact |
|---|---|---|
| Advanced Microphone Arrays | Capturing sound from multiple directions for immersive audio. | Enhanced spatial audio and recording quality. |
| AI-Driven Sound Analysis | Automatically classifying and analyzing sound events in urban environments. | Improved noise monitoring and soundscape management. |
| Sound Mapping | Creating visual representations of sound levels to identify noise hotspots. | Informed urban planning and noise reduction strategies. |
| Acoustic Design | Designing urban spaces to minimize noise and create pleasant sound environments. | Healthier and more enjoyable urban living. |
| Spatial Audio Recording | Capturing sound in three dimensions for immersive playback experiences. | Realistic and engaging audio experiences. |
| Noise Reduction | AI-powered tools that automatically reduce unwanted noise from recordings. | Cleaner and more professional-sounding audio. |
| Sound Classification | AI algorithms that can identify and categorize different types of sounds. | Efficient organization and retrieval of sound recordings. |
| Immersive Audio Experiences | Creating soundscapes that surround the listener for a more engaging experience. | Enhanced entertainment and therapeutic applications of sound. |
12. FAQ: Understanding the Speed of Sound
Here are some frequently asked questions about understanding the speed of sound.
12.1. What is the Speed of Sound in a Vacuum?
What is the speed of sound in a vacuum?
Sound cannot travel in a vacuum because it requires a medium (such as air, water, or solid) to propagate. A vacuum lacks the necessary particles to transmit sound waves.
12.2. How Does Altitude Affect the Speed of Sound?
How does altitude affect the speed of sound?
Altitude affects sound speed primarily through changes in temperature and air density; higher altitudes generally have lower temperatures, which decreases sound speed. The relationship between altitude, temperature, and sound speed is complex but generally follows the principles described earlier.
12.3. Can Sound Travel Faster Than the Speed of Light?
Can sound travel faster than the speed of light?
No, sound cannot travel faster than the speed of light. Light travels much faster than sound because it is an electromagnetic wave and does not require a medium to propagate.
12.4. What is the Speed of Sound in Different Gases?
What is the speed of sound in different gases?
The speed of sound varies in different gases depending on their molecular mass and temperature. Lighter gases generally have higher sound speeds.
12.5. How Does Humidity Affect the Speed of Sound?
How does humidity affect the speed of sound?
Humidity can slightly increase the speed of sound because water vapor is lighter than the nitrogen and oxygen molecules that make up most of the air. This effect is usually minor but can be noticeable in certain conditions.
12.6. What is the Range of Human Hearing?
What is the range of human hearing in terms of frequency?
The range of human hearing is typically between 20 Hz and 20,000 Hz. However, this range can vary with age and exposure to loud noises.
12.7. How Does the Speed of Sound Affect Musical Instruments?
How does the speed of sound affect musical instruments?
The speed of sound is critical in determining the pitch and tone of musical instruments. Instrument design relies on precise sound speed calculations to achieve desired acoustic properties.
12.8. What is the Speed of Sound in Human Tissue?
What is the approximate speed of sound in human tissue?
The approximate speed of sound in human tissue is around 1540 m/s. This value is important in medical imaging techniques like ultrasound.
12.9. How is the Speed of Sound Used in Medical Imaging?
How is the speed of sound used in medical imaging?
The speed of sound is used in medical imaging techniques like ultrasound to create images of internal organs and tissues. The time it takes for sound waves to reflect off different structures is used to create detailed images.
12.10. What is the Speed of Sound in Sea Water?
What is the approximate speed of sound in sea water?
The approximate speed of sound in sea water is around 1540 m/s. This value is higher than in fresh water due to the higher density and salinity of sea water.
Conclusion: Mastering Sound Wave Calculations
Understanding how to calculate the speed of a sound wave is essential for anyone working with sound, from audio engineers to urban planners. By grasping the underlying principles and utilizing resources like streetsounds.net, you can enhance your expertise and create innovative soundscapes.
Ready to take your sound explorations to the next level? Visit streetsounds.net to discover a world of high-quality street sounds, insightful articles, and a vibrant community of sound enthusiasts. Explore our extensive library, learn from expert interviews, and connect with fellow creators.
Address: 726 Broadway, New York, NY 10003, United States
Phone: +1 (212) 998-8550
Website: streetsounds.net
Start your sonic journey today and unleash the power of urban sound!
