The speed of sound in a medium is determined by the medium’s properties, particularly its elasticity and density, so understanding these factors is key, and that’s where streetsounds.net comes in. By exploring the science behind sound propagation and street sound dynamics, you can gain a deeper understanding of acoustic phenomena and their relationship to urban environments. This article will explore these concepts, reveal the formulas involved, and offer real-world examples to boost your understanding of urban acoustics.
1. What Is the Speed of Sound?
The speed of sound is the distance a sound wave travels through a medium in a given amount of time; it varies depending on the medium’s properties, such as density and elasticity.
Sound waves, like any other type of wave, have a certain speed, frequency, and wavelength. As you may have seen at a fireworks show ([Figure 1]), the speed of sound is easy to demonstrate. The flash of light from an explosion appears long before the sound or pressure wave hits you, showing that sound moves at a measurable pace, far slower than light.
In essence, the speed of a wave (v) is tied to its frequency (f) and wavelength (λ) by the following equation:
(v = fλ)
Here, (v) stands for the wave’s speed, (f) for its frequency, and (λ) for its wavelength. Remember that the wavelength is the space between two similar spots on the wave. For a sound wave, this is the distance between compressions. The frequency matches the sound’s source, measuring waves passing a point each second.
1.1. Primary Characteristics of Sound Waves
Understanding the primary characteristics of sound waves—speed, frequency, and wavelength—is crucial for anyone working with audio, whether in music production, sound engineering, or urban sound design. The interplay between these elements dictates how we perceive and manipulate sound.
1.2. How Does the Speed of Sound Relate to Streetsounds.net?
At streetsounds.net, understanding the speed of sound can enhance the quality and realism of your sound designs. By knowing how sound travels in different urban environments, you can create more accurate and immersive audio experiences. Whether you’re a sound engineer, filmmaker, or game designer, mastering these concepts can help you elevate your work.
2. What Factors Affect the Speed of Sound?
Several factors affect the speed of sound in a medium, including the medium’s density, elasticity, and temperature. Sound travels faster in denser, more elastic materials and generally increases with temperature.
The speed at which sound travels varies widely depending on the medium. The speed of sound in a medium is determined by how quickly vibrational energy can move through that medium. Therefore, figuring out the speed of sound means looking at both the medium and its state. Generally, you can find the speed of a mechanical wave in a medium using this formula:
(v = sqrt{frac{text{elastic property}}{text{inertial property}}})
This formula shows that the speed of sound depends on how elastic and how dense the medium is. Also, sound waves fit the wave equation:
(frac{partial^{2} y (x,t)}{partial x^{2}} = frac{1}{v^{2}} frac{partial^{2} y (x,t)}{partial t^{2}})
As a reminder, the speed of a wave on a string is (v = sqrt{frac{F_{T}}{mu}}), where (F_T) is the tension and (mu) is the linear density. Sound moves through a fluid at a speed determined by the bulk modulus (B) and density ((rho)):
(v = sqrt{frac{B}{rho}})
The speed of sound in a solid depends on Young’s modulus (Y) and density ((rho)):
(v = sqrt{frac{Y}{rho}})
In an ideal gas, the speed of sound is:
(v = sqrt{frac{gamma RT_{K}}{M}})
where (gamma) is the adiabatic index, (R = 8.31 , text{J/mol} cdot text{K}) is the gas constant, (T_K) is the absolute temperature in kelvins, and (M) is the molecular mass. The stiffer or less compressible a medium is, the faster sound travels. A denser medium means sound moves slower.
2.1. Influence of Medium Density
The density of a medium plays a crucial role in determining the speed of sound. Higher density generally leads to slower sound propagation because the increased mass resists the transmission of vibrational energy. This effect is particularly noticeable when comparing sound speeds in gases versus liquids or solids.
2.2. The Role of Elasticity
Elasticity, or a medium’s ability to return to its original shape after being deformed, significantly affects the speed of sound. More elastic materials allow sound to travel faster because they quickly restore their shape, facilitating faster energy transfer.
2.3. Temperature’s Effect on Sound Speed
Temperature also has a direct impact on the speed of sound. As temperature increases, the particles in a medium move faster, which allows sound waves to propagate more quickly. This is most noticeable in gases, where the relationship between temperature and sound speed is well-defined.
3. How to Calculate the Speed of Sound in Different Media
To calculate the speed of sound, you must consider the specific properties of the medium through which the sound is traveling. The formulas vary depending on whether the medium is a gas, liquid, or solid.
The speed of sound changes significantly depending on the medium, as shown in Table 1. The speed of sound relies on how well vibrational energy is transferred through the medium. Therefore, calculating the speed of sound depends on the medium and its condition. In general, the equation for the speed of a mechanical wave in a medium involves the square root of the restoring force, or elastic property, divided by the inertial property:
(v = sqrt{frac{text{elastic property}}{text{inertial property}}})
Sound waves also follow the wave equation:
(frac{partial^{2} y (x,t)}{partial x^{2}} = frac{1}{v^{2}} frac{partial^{2} y (x,t)}{partial t^{2}})
Recall that the speed of a wave on a string is (v = sqrt{frac{F_{T}}{mu}}), where the restoring force is the tension (F_T), and the inertial property is the linear density (mu). In a fluid, the speed of sound depends on the bulk modulus and the density:
(v = sqrt{frac{B}{rho}})
In a solid, the speed of sound depends on Young’s modulus and the density:
(v = sqrt{frac{Y}{rho}})
For an ideal gas, the speed of sound is:
(v = sqrt{frac{gamma RT_{K}}{M}})
where (gamma) is the adiabatic index, (R = 8.31 , text{J/mol} cdot text{K}) is the gas constant, (T_K) is the absolute temperature in kelvins, and (M) is the molecular mass. Generally, the more rigid (or less compressible) the medium, the faster the speed of sound. This is similar to how the frequency of simple harmonic motion is directly related to the stiffness of an oscillating object, measured by the spring constant (k). The greater the density of a medium, the slower the speed of sound. This is like how the frequency of simple harmonic motion is inversely related to the mass (m) of the oscillating object. The speed of sound in air is slow because air is easily compressed. Liquids and solids are relatively rigid and hard to compress, so the speed of sound in them is usually greater than in gases.
3.1. Calculating Sound Speed in Gases
In gases, the speed of sound is calculated using the formula (v = sqrt{frac{gamma RT}{M}}), where (gamma) is the adiabatic index, (R) is the gas constant, (T) is the absolute temperature in Kelvin, and (M) is the molar mass of the gas.
3.2. Calculating Sound Speed in Liquids
For liquids, the speed of sound is determined by (v = sqrt{frac{B}{rho}}), where (B) is the bulk modulus of the liquid, and (rho) is its density. The bulk modulus measures the liquid’s resistance to uniform compression.
3.3. Calculating Sound Speed in Solids
In solids, the speed of sound can be calculated using (v = sqrt{frac{Y}{rho}}), where (Y) is Young’s modulus of the solid, and (rho) is its density. Young’s modulus measures the solid’s stiffness or resistance to deformation under stress.
4. Formulas for Calculating Speed of Sound
Several formulas are used to calculate the speed of sound in different media, depending on the properties of the medium. These include formulas for gases, liquids, and solids, each accounting for different material characteristics.
Because the speed of sound depends on the material’s density, which in turn depends on temperature, there is a relationship between temperature and the speed of sound in a given medium. For air at sea level, the speed of sound is given by:
(v = 331 , text{m/s} sqrt{1 + frac{T{C}}{273 , text{°C}}} = 331 , text{m/s} sqrt{frac{T{K}}{273 , text{K}}})
where the temperature in the first equation ((T_C)) is in degrees Celsius, and the temperature in the second equation ((T_K)) is in kelvins. The speed of sound in gases is related to the average speed of particles in the gas:
(v{rms} = sqrt{frac{3k{B}T}{m}})
where (kB) is the Boltzmann constant ((1.38 times 10^{-23} , text{J/K})), and (m) is the mass of each (identical) particle in the gas. Note that (v) refers to the coherent propagation speed of a disturbance (the wave), whereas (v{rms}) describes the speeds of particles in random directions. Thus, it is reasonable that the speed of sound in air and other gases should depend on the square root of temperature. While not negligible, this is not a strong dependence. At (0 , text{°C}), the speed of sound is (331 , text{m/s}), whereas at (20.0 , text{°C}), it is (343 , text{m/s}), less than a (4%) increase.
4.1. Speed of Sound Formula in Air
The speed of sound in air is commonly approximated using the formula (v = 331.4 + 0.6T), where (v) is the speed of sound in meters per second, and (T) is the temperature in degrees Celsius.
4.2. General Formula for Ideal Gases
In ideal gases, the speed of sound is calculated using (v = sqrt{frac{gamma RT}{M}}), where (v) is the speed of sound, (gamma) is the adiabatic index, (R) is the gas constant, (T) is the absolute temperature in Kelvin, and (M) is the molar mass.
4.3. Formula for Liquids and Solids
For liquids and solids, the speed of sound is calculated using (v = sqrt{frac{K}{rho}}), where (v) is the speed of sound, (K) is the bulk modulus (for liquids) or Young’s modulus (for solids), and (rho) is the density.
5. Examples of Speed of Sound Calculations
Applying the formulas for calculating the speed of sound in different media helps illustrate how these principles work in practice. These examples cover various scenarios, including air, water, and solids, providing a comprehensive understanding.
Table 1: Speed of Sound in Various Media
| Medium | Speed (m/s) |
|---|---|
| Gases at 0°C | |
| Air | 331 |
| Carbon dioxide | 259 |
| Oxygen | 316 |
| Helium | 965 |
| Hydrogen | 1290 |
| Liquids at 20°C | |
| Ethanol | 1160 |
| Mercury | 1450 |
| Water, fresh | 1480 |
| Sea water | 1540 |
| Human tissue | 1540 |
| Solids | |
| Vulcanized rubber | 54 |
| Polyethylene | 920 |
| Marble | 3810 |
| Glass, Pyrex | 5640 |
| Lead | 1960 |
| Aluminum | 5120 |
| Steel | 5960 |
5.1. Example: Calculating Sound Speed in Air
To calculate the speed of sound in air at 25°C, use the formula (v = 331.4 + 0.6T). Substituting (T = 25), we get (v = 331.4 + 0.6(25) = 346.4) m/s.
5.2. Example: Calculating Sound Speed in Water
For water at 20°C, the bulk modulus (B) is approximately (2.2 times 10^9) Pa, and the density (rho) is (1000) kg/m³. Using (v = sqrt{frac{B}{rho}}), we find (v = sqrt{frac{2.2 times 10^9}{1000}} approx 1483) m/s.
5.3. Example: Calculating Sound Speed in Steel
In steel, Young’s modulus (Y) is about (200 times 10^9) Pa, and the density (rho) is (7850) kg/m³. Using (v = sqrt{frac{Y}{rho}}), we get (v = sqrt{frac{200 times 10^9}{7850}} approx 5047) m/s.
6. Real-World Applications of Speed of Sound Calculations
Understanding the speed of sound has numerous practical applications in various fields, including acoustics, engineering, and environmental science. From designing concert halls to studying seismic activity, these calculations are essential.
One of sound’s more important qualities is that its speed is almost the same no matter the frequency. This is generally true in open air for audible sounds. If this weren’t true, you would notice it when listening to a marching band in a football stadium. If high-frequency sounds traveled faster, the farther you were from the band, the more the low-pitch instruments would lag behind the high-pitch ones. But because the music from all instruments arrives in cadence regardless of distance, all frequencies must travel at nearly the same speed. Remember that:
(v = fλ)
In a set medium, (v) is constant, creating a relationship between (f) and (λ): the higher the frequency, the smaller the wavelength.
6.1. Architectural Acoustics
Architects use speed of sound calculations to design spaces with optimal sound quality. Understanding how sound waves behave in different materials helps in creating concert halls, theaters, and studios with excellent acoustics.
6.2. Underwater Acoustics
In underwater acoustics, knowing the speed of sound in water is crucial for sonar systems and underwater communication. These calculations help in locating objects and mapping the ocean floor.
6.3. Geophysics and Seismology
Geophysicists use the speed of sound to study Earth’s structure. Seismic waves, which are essentially sound waves in Earth’s crust, are affected by the rigidity of the medium. Earthquakes produce both longitudinal and transverse waves that travel at different speeds. The bulk modulus of granite is greater than its shear modulus. For that reason, the speed of longitudinal or pressure waves (P-waves) in earthquakes in granite is significantly higher than the speed of transverse or shear waves (S-waves). Both types of earthquake waves travel slower in less rigid material, such as sediments. P-waves have speeds of 4 to 7 km/s, and S-waves range in speed from 2 to 5 km/s, both being faster in more rigid material. The P-wave gets progressively farther ahead of the S-wave as they travel through Earth’s crust. The time between the P- and S-waves is routinely used to determine the distance to their source, the epicenter of the earthquake. Because S-waves do not pass through the liquid core, two shadow regions are produced.
Analyzing the speed and behavior of these waves provides insights into the composition and structure of the Earth’s layers.
6.4. Streetsounds.net and Urban Planning
At streetsounds.net, understanding the speed of sound is vital for urban planning projects. By considering how sound travels in urban environments, planners can design cities that minimize noise pollution and enhance the quality of life for residents.
6.5. Practical Example: Calculating Wavelengths
Calculate the wavelengths of sounds at the extremes of the audible range, 20 and 20,000 Hz, in 30.0 °C air. (Assume that the frequency values are accurate to two significant figures.)
Strategy
To find wavelength from frequency, we can use (v = fλ).
Solution
-
Identify knowns. The value for (v) is given by
(v = 331 , text{m/s} sqrt{frac{T}{273 , text{K}}}) -
Convert the temperature into kelvins and then enter the temperature into the equation
(v = 331 , text{m/s} sqrt{frac{303 , text{K}}{273 , text{K}}} = 348.7 , text{m/s}) -
Solve the relationship between speed and wavelength for (λ):
(λ = frac{v}{f}) -
Enter the speed and the minimum frequency to give the maximum wavelength:
(λ_{max} = frac{348.7 , text{m/s}}{20 , text{Hz}} = 17 , text{m})
-
Enter the speed and the maximum frequency to give the minimum wavelength:
(λ_{min} = frac{348.7 , text{m/s}}{20,000 , text{Hz}} = 0.017 , text{m} = 1.7 , text{cm})
Because the product of (f) multiplied by (λ) equals a constant, the smaller (f) is, the larger (λ) must be, and vice versa.
6.6. Sound Behavior Across Mediums
The speed of sound can change when sound travels from one medium to another, but the frequency usually remains the same. This is similar to how the frequency of a wave on a string is equal to the frequency of the force oscillating the string. If (v) changes and (f) remains the same, then the wavelength (λ) must change. That is, because (v = fλ), the higher the speed of a sound, the greater its wavelength for a given frequency.
7. How Bats Use the Speed of Sound
Bats use echolocation to navigate and hunt, relying on their ability to emit sound waves and interpret the returning echoes. Their use of sound and its speed is a fascinating example of how understanding these principles can be applied in nature.
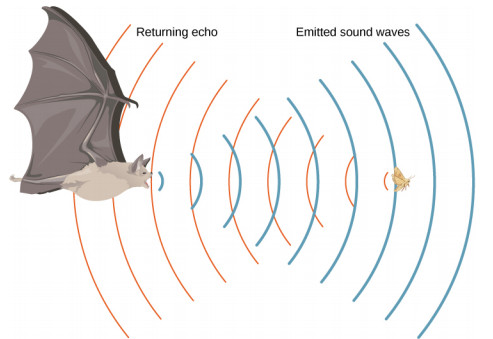A bat emitting sound waves to detect a flying insect through echolocation.
Bats use sound echoes to find their way and catch prey. The time it takes for the echo to return is directly related to the distance.
7.1. Echolocation Explained
Echolocation involves emitting high-frequency sounds and listening for the echoes that bounce back from objects in the environment. By analyzing the time delay and characteristics of the echoes, bats can determine the location, size, and shape of objects.
7.2. Calculating Distance Using Sound Speed
Bats calculate the distance to an object by measuring the time it takes for the echo to return and using the formula (d = frac{vt}{2}), where (d) is the distance, (v) is the speed of sound, and (t) is the time delay. The division by 2 accounts for the sound traveling to the object and back.
7.3. Relevance to Streetsounds.net
Understanding how bats use sound to navigate can inspire new technologies and techniques in urban sound design. By mimicking the principles of echolocation, engineers can develop advanced sensing and navigation systems for urban environments, an area that streetsounds.net is keen to explore.
8. The Derivation of the Speed of Sound in Air
The speed of sound in air can be derived from basic physical principles, including mass flow rate, continuity equations, and thermodynamic processes. This derivation provides a deeper understanding of the factors influencing sound propagation.
As mentioned, the speed of sound in a medium depends on the medium and its state. Deriving the equation for the speed of sound in air starts with the mass flow rate and the continuity equation. Consider fluid flow through a pipe with cross-sectional area (A) ([Figure 4]). The mass in a small volume of length (x) of the pipe is equal to the density times the volume, or:
(m = rho V = rho Ax)
The mass flow rate is:
(frac{dm}{dt} = frac{d}{dt} (rho V) = frac{d}{dt} (rho Ax) = rho A frac{dx}{dt} = rho Av)
The continuity equation states that the mass flow rate into a volume has to equal the mass flow rate out of the volume:
(rho{in} A{in}v{in} = rho{out} A{out}v{out})
8.1. Mass Flow Rate and Continuity Equation
The derivation starts with the mass flow rate, which describes the amount of mass moving through a cross-sectional area per unit time. The continuity equation ensures that mass is conserved in the system.
8.2. Thermodynamic Processes
The derivation also involves thermodynamic processes, particularly adiabatic processes, where no heat is added or removed from the system. This is crucial for understanding how pressure and density changes affect the speed of sound.
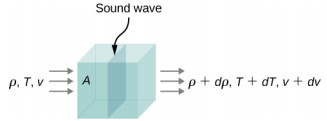Schematic showing fluid flow through a pipe, illustrating mass flow rate and continuity.
The mass of a fluid in a volume equals the density times the volume, (m = rho V = rho Ax). The mass flow rate is the time derivative of the mass.
8.3. Steps in the Derivation
- Consider a Parcel of Air: Imagine a small volume of air with density (rho), temperature (T), and velocity (v). On the other side, these properties change to (rho + drho), (T + dT), and (v + dv).
- Apply the Continuity Equation: The continuity equation states that the mass flow rate entering the volume equals the mass flow rate leaving the volume:
(rho Av = (rho + drho)A(v + dv))
This simplifies to:
(rho , dv = -v , drho) - Net Force Calculation: The net force on the volume of fluid equals the sum of the forces on the left and right faces:
(F_{net} = -dp , dy , dz)
Using (ma = -dp , dy , dz), we find:
(rho v , dv = -dp) - Adiabatic Process: For an adiabatic process, (pV^gamma = text{constant}), where (p) is pressure, (V) is volume, and (gamma) is a constant (1.40 for air).
- Ideal Gas Law: Assuming air is an ideal gas, use the ideal gas law:
(p = rho frac{RT}{M})
where (M) is the molar mass of air. - Final Equation: Combining these steps, the speed of sound (v) is derived as:
(v = sqrt{frac{gamma RT}{M}})
8.4. Significance of the Derivation
This derivation highlights the importance of thermodynamic principles and fluid dynamics in understanding sound propagation. It also shows how the speed of sound is intrinsically linked to the properties of the air, such as temperature and density.
9. Sound Waves in Solids: Longitudinal and Transverse
While sound waves in fluids are longitudinal, sound waves in solids can travel as both longitudinal and transverse waves, each with different speeds and characteristics.
Although sound waves in a fluid are longitudinal, sound waves in a solid travel both as longitudinal waves and transverse waves. Seismic waves, which are essentially sound waves in Earth’s crust produced by earthquakes, are an interesting example of how the speed of sound depends on the rigidity of the medium.
9.1. Longitudinal Waves (P-waves)
Longitudinal waves, also known as pressure waves or P-waves, involve particles vibrating parallel to the direction of wave propagation. They travel faster than transverse waves and can propagate through solids, liquids, and gases.
9.2. Transverse Waves (S-waves)
Transverse waves, or shear waves (S-waves), involve particles vibrating perpendicular to the direction of wave propagation. They can only travel through solids because liquids and gases cannot support shear stress.
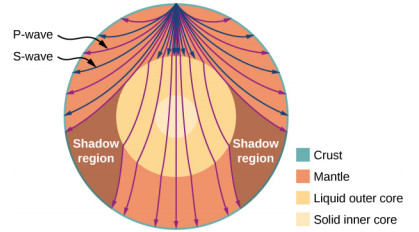Illustration showing P and S waves from an earthquake and shadow regions due to the liquid core.
Earthquakes produce both longitudinal waves (P-waves) and transverse waves (S-waves), and these travel at different speeds. S-waves cannot travel through the liquid core, creating shadow regions.
9.3. Differences in Speed and Propagation
The speed of P-waves is typically higher than that of S-waves due to the different modes of particle vibration and the material properties that affect their propagation. This difference in speed is used in seismology to determine the distance to earthquake epicenters.
9.4. Application in Seismology
Seismologists use the different speeds of P- and S-waves to study the Earth’s internal structure. The waves’ behavior as they pass through different layers of the Earth provides valuable information about the composition and physical state of these layers.
10. Intensity and Distance from the Source
As sound waves move away from a source, their power per unit area, known as intensity, decreases. This principle explains why sounds are louder near the source and become fainter as you move away.
As sound waves move away from a speaker, or away from the epicenter of an earthquake, their power per unit area decreases. This is why the sound is very loud near a speaker and becomes less loud as you move away from the speaker. This also explains why there can be an extreme amount of damage at the epicenter of an earthquake but only tremors are felt in areas far from the epicenter. The power per unit area is known as the intensity.
10.1. The Inverse Square Law
The intensity of sound decreases with the square of the distance from the source, following the inverse square law. Mathematically, this is expressed as (I propto frac{1}{r^2}), where (I) is the intensity, and (r) is the distance from the source.
10.2. Practical Implications
This principle has significant implications for sound design and urban planning. Understanding how sound intensity diminishes with distance allows engineers and planners to design spaces that manage noise levels effectively.
10.3. Example: Sound Levels in Urban Environments
In urban environments, sound levels can vary dramatically depending on the distance from noise sources such as traffic, construction sites, and music venues. Understanding the inverse square law helps in predicting and mitigating noise pollution in these areas.
10.4. Streetsounds.net and Noise Mapping
At streetsounds.net, we use the principles of sound intensity and distance to create detailed noise maps of urban environments. These maps help identify noise hotspots and inform strategies for reducing noise pollution, contributing to healthier and more livable cities.
11. Conclusion: The Importance of Understanding Sound Speed
Understanding how to calculate the speed of sound in various mediums is essential for diverse applications, from designing acoustic spaces to analyzing seismic activity. By grasping the underlying principles and formulas, you can gain deeper insights into the behavior of sound in different environments.
Whether you’re fine-tuning the acoustics of a concert hall or mapping the unique soundscapes of city streets, the principles of sound speed are indispensable. By considering the properties of different media—be it air, water, or solid materials—you can more effectively predict and manipulate sound behavior to suit your creative and practical needs.
Imagine you observe two firework shells explode. You hear the explosion of one as soon as you see it. However, you see the other shell for several milliseconds before you hear the explosion. Explain why this is so.
12. Explore the Sounds of the Streets at Streetsounds.net
Ready to explore the dynamic world of sound? Visit streetsounds.net to discover a rich library of street sound effects, insightful articles, and a community of fellow sound enthusiasts. Whether you’re creating immersive soundscapes or seeking inspiration, streetsounds.net is your ultimate resource for urban audio.
- Discover the sounds of New York: Immerse yourself in the soundscapes of one of the world’s most vibrant cities.
- Connect with our community: Exchange ideas with sound artists, filmmakers, and urban enthusiasts from around the globe.
- Stay updated: Access the latest articles, tutorials, and resources on sound design and urban acoustics.
Address: 726 Broadway, New York, NY 10003, United States
Phone: +1 (212) 998-8550
Website: streetsounds.net
13. FAQ: Understanding the Speed of Sound
13.1. What is the main factor affecting the speed of sound in air?
The main factor affecting the speed of sound in air is temperature; as temperature increases, the speed of sound also increases.
13.2. Does the speed of sound differ in water compared to air?
Yes, the speed of sound is significantly faster in water (around 1480 m/s in fresh water) than in air (around 343 m/s at room temperature).
13.3. How does density influence the speed of sound?
Generally, the speed of sound decreases as the density of the medium increases, although this also depends on the medium’s elasticity.
13.4. Can sound travel in a vacuum?
No, sound cannot travel in a vacuum because it requires a medium (such as air, water, or solids) to propagate.
13.5. What is the formula for calculating the speed of sound in an ideal gas?
The formula is (v = sqrt{frac{gamma RT}{M}}), where (v) is the speed of sound, (gamma) is the adiabatic index, (R) is the gas constant, (T) is the absolute temperature in Kelvin, and (M) is the molar mass.
13.6. Why do musicians and sound engineers need to understand the speed of sound?
Musicians and sound engineers need to understand the speed of sound for tasks such as timing audio effects, designing acoustic spaces, and synchronizing audio with visual media.
13.7. How is the speed of sound used in medical applications?
In medical applications, ultrasound imaging uses the speed of sound to create images of internal organs and tissues, helping diagnose and monitor various medical conditions.
13.8. What role does elasticity play in determining the speed of sound in a medium?
Elasticity is crucial because it determines how quickly a medium returns to its original shape after being deformed by a sound wave. Higher elasticity generally leads to a faster speed of sound.
13.9. How do seismic waves relate to the speed of sound?
Seismic waves are essentially sound waves that travel through the Earth. Their speed is used to study the Earth’s internal structure, with different wave types traveling at varying speeds depending on the material they pass through.
13.10. Why is the speed of sound important for urban planning and noise control?
Understanding the speed of sound is crucial for urban planning as it helps in designing spaces that minimize noise pollution and optimize acoustic environments, contributing to the well-being of city residents.
